矩阵的基本概念 #
矩阵的基本运算 #
若向量$a,b$,则它的内积、外积定义如下:
| inner product | $\sum a_ib_i$ | $a\odot b$ |
| Outer product | $ab^T$ | $a\otimes b$ |
Hardmard积、Kronnecker积和矩阵乘法 #
若矩阵$A\in R^{m\times n},B\in R^{m\times n}$,则它的哈达玛积、克罗内亚积如下:
| Hardmard Product | 逐元素相乘 | $A\circ B \in R^{m\times n}$ |
| Kronnecker Product | 矩阵A每个元素乘以矩阵B | $A\otimes B \in R^{m^2\times n^2}$ |
| Matrix Product | 矩阵乘法 | $A\cdot B$ or $AB$ |
矩阵乘法一般情况下不满足交换律,但也有例外:
- A、B中任一是单位阵、数量阵、零矩阵,或者A、B均为对角阵时,满足$AB=BA$
- A、B互为逆矩阵、正交矩阵、酉矩阵时,满足交换律$AB=BA$
- 当$AB=BA$时
- $(A+B)(A-B)$满足交换律
- $(A+B)^m$可使用二项式定理展开
直和 #
矩阵的直和定义如下:
$$A\oplus B=\begin{bmatrix}A\quad O\newline O\quad B\end{bmatrix}$$
逆矩阵 #
- 求解思路:
- 直接求逆,推导出逆矩阵
- 构造$AA^{-1}=I$(一般移项后对A作因式分解)
- 特殊构造
- 当A、B可逆时,注意构造$AA^{-1}$和$BB^{-1}$
- 当A正交时,注意$A^{-1}=A^T$
广义逆 #
| 左逆和右逆 | 左逆矩阵满足$LA=I$;右逆矩阵满足$AR=I$ | |
| 左伪逆和右伪逆 | 列满秩矩阵的左伪逆矩阵$L=(A^HA)^{-1}A^H$;行满秩矩阵的右伪逆矩阵$R=A^H(AA^H)^{-1}$ | 列满秩则有$A^HA$可逆;行满秩则有$AA^H$可逆 |
| M-P广义逆 | 若矩阵G满足$AGA=A或GAG=G或(AG)^T=AG或(GA)^T=GA$,则称矩阵G是加号逆或M-P广义逆 特别地,若$AA^-A=A$,则称$A^-$是$A$的广义逆矩阵 $A^{-1},L,R$都是A的广义逆矩阵 |
秩、行列式、迹 #
秩 #
线性映射定义
考虑线性映射$f_A:F^n\rightarrow F^m$在某一组基下的表示$x\rightarrow Ax$,则$A$的秩定义为$f_A$的象空间的维度,而核空间的维度则定义为$n-r(A)$
| 性质 | 证明/推论 | |
|---|---|---|
| $r(AB)\le\min(r(A),r(B))$ | 考虑矩阵的线性映射,一方面,$ABx$将$Bx$投射到$A$的象空间,因此$r(AB)\le r(A)$;另一方面,$ABx$是$Bx$基向量的线性组合,因此$r(AB)\le r(B)$ 若A满秩,则$r(AB)=r(B)$ |
|
| $r(A)+r(B)-n\le r(AB)$ | Frobeinus不等式$r(AB)+r(BC)\le r(B)+r(ABC)$ | |
| $r(A+B)\le r(A)+r(B)$ | 秩为k的矩阵可以分解为k个秩1矩阵的和 | |
| $r(A^TA)=r(AA^T)=r(A)=r(A^T)$ | 转置不变性 |
含参矩阵:根据矩阵的秩,确定参数的范围
-
秩为1,则每一行线性相关,即系数成比例(可据此推导出系数关系)
-
矩阵满秩/秩的分类讨论($\alpha,\beta$)
将向量组排列成矩阵,用每一行消去一个维度(注意消去不含参的维度),保证剩下的两行线性无关/相关
行列式 #
拉普拉斯展开:行列式可以按某一行或列展开为元素与其代数余子式的乘积和,即$|B|=\sum_j b_{ij}C_{ij}$,其中代数余子式$C_{ij} = (−1)^{i + j}M_{ij}$
$$ 考虑矩阵B= \begin{bmatrix} 1\quad2\quad3\newline 4\quad5\quad6\newline 7\quad8\quad9\newline \end{bmatrix} \newline 它的行列式|B|= 1\cdot \begin{vmatrix} 5\quad6\newline 8\quad9\newline \end{vmatrix} -2\cdot \begin{vmatrix} 4\quad6\newline 7\quad9\newline \end{vmatrix} +3\cdot \begin{vmatrix} 4\quad5\newline 7\quad8\newline \end{vmatrix} $$
迹 #
| 性质 | 推论 | |
|---|---|---|
| 线性性质 | $tr(A+B)=tr(A)+tr(B)$ | |
| $tr(r\cdot A)=r\cdot tr(A)$ | ||
| $tr(A)=tr(A^T)$ | ||
| 矩阵乘积 | 若交换后乘积仍然存在,则有$tr(AB)=tr(BA)$ | $tr(ABC)=tr(BCA)=tr(CAB)\ne tr(ACB)$ |
| $tr(AB)=\sum_{ij}a_{ij}b_{ji}$ | $tr(A^TB)=\sum_{i,j}a_{ij}b_{ij}=vec^T(A)\cdot vec(B)$ | |
| 相似不变性 | $tr(B)=tr(PAP^{-1})=tr(A)$ |
- $tr(XX^T)=\sum |x_{ij}|^2$,多天线发射信号矩阵的功率
范数 #
向量范数 #
向量的p范数$||x||_p=(\sum_i |x_i|^p)^{1/p}$
特别地,当$p\rightarrow\infty$时,称为无穷范数,返回向量的最大元素$max(x_i)$
矩阵范数 #
矩阵范数 - 维基百科,自由的百科全书 (wikipedia.org)
矩阵的元素范数和诱导范数都可以记为也记为$A||_p$
矩阵的元素范数 #
矩阵的元素范数也称为$L_p$范数,$||A||_p = ( \sum |aij|^p )^{1/p}$
特别地,$L_2$范数也被称为Frobenius范数,记为$||A||_F$
当$p\rightarrow\infty$时,称为极大值范数,返回矩阵的最大元素$max(a_{ij})$
范数的性质 #
| 矩阵范数 | 向量范数 | |
|---|---|---|
| 三角不等式 | $||A+B||\le||A||+||B||$ | $||u+v||\le||u||+||v||$ |
| Cauchy不等式 | $||AB||\le||A||\cdot||B||$ | $||uv||\le||u||\cdot||v||$ |
矩阵的诱导范数 #
向量$x$的p范数的缩放倍率的最大值,有$||A||_p=\max{\frac{||Ax||_p}{||x||_p}}$
特别地,诱导2范数是矩阵A的最大奇异值。
随机向量 #
| 自相关矩阵 | $R_x=E[(x(\xi)x^H(\xi))]$ | |
| 互相关矩阵 | $R_{xy}=E[(x(\xi)y^H(\xi))]$ | |
| 自协方差矩阵 | $C_x=E([x(\xi)-\mu][x(\xi)-\mu]^T)$ | $C_x=R_x-\mu_x\mu_x^T$ |
| 互协方差矩阵 | $C_x=E([x(\xi)-\mu_x][y(\xi)-\mu_y]^T)$ |
高斯随机向量 #
设高斯随机向量$x(t)=[x_1(t),\dots,x_N(t)]^T$服从多维正态分布$N(\mu,C_x)$,均值向量$\mu=[\mu_1,\dots,\mu_N]^T$若各个维度独立,则有协方差矩阵$C_x=diag{\sigma_1^2,\dots,\sigma_N^2}$,概率密度函数$f(x)=\frac{1}{(2\pi)^{N/2}det(C_x)^{1/2}}exp(-\frac{1}{2}(x-\mu)^TC_x^{-1}(x-\mu))$
随机误差向量 #
误差向量的每个维度期望为0,但功率不为0(因为正负相互抵消,平方后累积)
特殊矩阵 #
基本矩阵 #
| 推广 | ||
|---|---|---|
| 基本矩阵 | $E_{mn}=e_me_n^T$是第m行第n列的元素为1的矩阵, 其中$e_n$是第n个元素为1的单位向量 |
|
| I型基本矩阵 | $E_{(p,q)}$ | 互换矩阵 选择矩阵 置换矩阵 |
| II型基本矩阵 | $E_{\alpha(p)}$ | |
| III型基本矩阵 | $E_{(p)+\alpha(q)}$ |
三角阵、对角阵 #
| 逆矩阵 | 行列式 | |
|---|---|---|
| 上/下三角阵 | 上/下三角阵 | $det(A)=\prod_i^Na_{ii}$ |
| 对角阵 | 对角阵 | $det(A)=\prod_i^Na_{ii}$ |
- 若矩阵是三角阵,又是酉矩阵,则矩阵是对角阵,且对角线元素的范数(绝对值)为1
- 若矩阵是上三角分块酉矩阵,$A=\begin{bmatrix}P\quad B\newline 0\quad Q\end{bmatrix}$,那么P、Q都是酉矩阵,且B=0
上/下三角阵的和、积仍然是上/下三角阵。
对称、正定、正交、正规 #
| 实空间 | 复空间 | 常见举例 | 性质 | |
|---|---|---|---|---|
| 对称矩阵 | $A^T=A$ | $A^H=A$ (Hermitian阵) |
||
| 正定矩阵 | $x^TAx>0$ | $x^HAx>0$ (前提先是对称阵) |
各阶顺序主子式>0(左上角行列式>0) | 特征值是正数 |
| 正交矩阵 | $QQ^T=Q^TQ=I$ | $UU^H=U^HU=I$ (酉矩阵) |
||
| 正规矩阵 | $A^TA=AA^T$ | $A^HA=AA^H$ | 必可以酉对角化 |
正规矩阵
-
实空间的对称矩阵、斜对称矩阵、正交矩阵是正规的;复空间的Hermitian阵、斜Hermitian阵、酉矩阵是正规矩阵
-
正规矩阵必可以酉对角化
-
若$A$是反对称矩阵,则$I+A,I-A,A-I$是非奇异的
正定矩阵
- 正定矩阵可以酉对角化,进而分解成n个正定的秩1矩阵的和,也可以开平方根,$B=B^{\frac{1}{2}}(B^{\frac{1}{2}})^H$,且$I=B^{\frac{1}{2}}B^{-\frac{1}{2}}$
- 若$A,B$为正定矩阵,则哈达玛积$AB$正定,若$A,B$为半正定矩阵,则哈达玛积$AB$半正定
- 若$A$是半正定矩阵,且非奇异,则$A$是正定矩阵
相似与相合 #
| 定义 | 性质 | |
|---|---|---|
| 相似矩阵 | $B=S^{-1}AS$ | 特征值相同 |
| 相合矩阵 | $B=C^HAC$ | 二次型函数相吻合 |
中心化矩阵 #
求和矩阵$J_N=\begin{bmatrix}1\quad\dots\quad1\newline\dots\newline1\quad\dots\quad1\newline\end{bmatrix}$,$J_NX$表示将矩阵$X$的每个向量表示为N个向量的和
中心化矩阵$C_N = I_N - \frac{1}{N}J_N$,$C_NX$表示矩阵X的每个向量减去这N个向量的均值
- 信号直流功率、交流功率的计算
Vandermonde矩阵 #
$$ A= \begin{bmatrix} a_1^0\ a_2^0\ \dots\ a_N^0\newline a_1\ a_2\ \dots\ a_N\newline \vdots \newline a_1^{N-1}\ a_2^{N-1}\ \dots\ a_N^{N-1}\newline \end{bmatrix} $$
行列式$det(A)=\prod_{i,j}^N(a_i-a_j)$
-
多项式插值中,线性方程组的系数矩阵是Vandermonde矩阵;易知,当$a_i\ne a_j$时,范德蒙矩阵是满秩的,存在唯一解
-
P个入射信号、N个阵元的信号响应矩阵是N*P维Vandermonde矩阵,其中阵元的响应强度随距离成指数级上升(0到N-1),而不同的入射信号对应不同的夹角($a_i$)。
-
Fourier矩阵也是一种特殊的vandermonde矩阵,指数在频率和时间两个方向都递增。DFT可以写成复空间上的内积$y(k)=\sum_{n=0}^{N-1} x(n)e^{-j\frac{2\pi kn}{N}}= <x,f_k> = f_k^H x$,其中$f_k=[1,e^{-j\frac{2\pi k}{N}},\dots,e^{-j\frac{2\pi k(N-1)}{N}}]$
矩阵函数与优化 #
矩阵函数 #
矩阵函数是通过矩阵的加法和乘法来定义的,而对于指数函数和三角函数,则是通过推广标量函数的幂级数展开来定义。
方法1:当矩阵是幂等矩阵时,可以将幂级数中的累加项合并,并利用指数函数的展开式来化解一系列系数的求和。
$A=\begin{bmatrix}1\quad 1\newline0\quad 0\end{bmatrix},B=\begin{bmatrix} 1\quad 1\newline0\quad 0\end{bmatrix}$,求$e^A,e^B,e^{A+B}$
A是幂等阵,$A^2=A$,进而$A^n=A$
由幂级数展开知$e^A=I+(\frac{1}{1!}+\frac{1}{2!}+\dots)A$ ,再根据$e=(1+\frac{1}{1!}+\frac{1}{2!}+\dots)$进一步化简,得$e^A=I+(e-1)A$
同理可得$e^B=I+(e-1)B$
根据幂级数展开$e^{A+B}=I+\sum_i\frac{1}{i!}(A+B)^i$ 因为$A+B= \begin{bmatrix} 2\quad 0\newline 0\quad 0 \end{bmatrix}$,所以$(A+B)^k=2^k(A+B)$ ,继而$e^{A+B}=I+\sum_{k=1}\frac{2^k}{k!}(A+B)$ ,根据$e^2=\sum_{k=0}\frac{2^k}{k!}$,化简得$e^{A+B}=I+(e^2-1)(A+B)$
- 当矩阵乘法可交换时,指数函数和三角函数才满足一些交换的性质,故$e^{A+B}$不能直接使用幂的乘法
方法2:将矩阵对角化,矩阵的幂级数,即,将对角线上的各个元素代入幂级数的原函数。
如果矩阵可对角化为$P^{-1}AP=\Lambda$,则有:
$e^A=Pdiag(e^{\lambda_1},\dots,e^{\lambda_n})P^{-1}$
$e^{tA}=Pdiag(e^{\lambda_1t},\dots,e^{\lambda_nt})P^{-1}$
$sinA=Pdiag(sin\lambda_1,\dots,sin{\lambda_n})P^{-1}$
矩阵的求导与微分 #
实值函数的自变量和因变量都可以是标量、向量、矩阵。
| 函数(因变量) | 向量变元$\mathbf{x}\in R^m$ | 矩阵变元$X\in R^{m\times n}$ |
|---|---|---|
| 标量函数$f\in R$ | $f:R^m\rightarrow R^{m\times n}$ | $f:R^{m\times n}\rightarrow R$ |
| 向量函数$f\in R^p$ | $f(\mathbf{x})\newline f:R^m\rightarrow R^p$ | $f(X)\newline f:R^{m\times n}\rightarrow R^p$ |
| 矩阵函数$f\in R^{p\times q}$ | $F(\mathbf{x})\newline f:R^m\rightarrow R^{p\times q}$ | $F(X)\newline f:R^{m\times n}\rightarrow R^{p\times q}$ |
偏导 #
标量函数的偏导 #
| 偏导 | 对变元的操作 | 符号 |
|---|---|---|
| 行向量偏导 | 将矩阵X行向量化(先列向量化,再转置) | $D_{vec^T(X)}f(X)=\frac{\partial f(X)}{\partial vec^T(X)}$ |
| Jacobian矩阵 | 将矩阵X转置 | $D_Xf(X)=\frac{\partial f(X)}{\partial X^T}$ |
| 列向量偏导 | 将矩阵X列向量化 | $\nabla_{vec(X)}f(X)=\frac{\partial f(X)}{\partial vec(X)}$ |
| 梯度矩阵 | 矩阵X不变 | $\nabla_Xf(X)=\frac{\partial f(X)}{\partial X}$ |
行向量偏导与Jacobian矩阵的关系 #
行向量偏导$vec^T(X)=[vec(X)]^T$和Jacobian矩阵$X^T$是不同的,行向量偏导实际上并没有对$X$作转置,如果需要将jacobian矩阵转化为行向量偏导的形式,则需要$rvec(X)=vec^T(X^T)$
矩阵/向量函数的Jacobin矩阵和梯度矩阵 #
首先向量/矩阵函数列向量化,再转置为行向量,然后求偏导,即为矩阵变元函数的Jacobian矩阵,记为$D_XF(X)$
如果是列向量偏导,则认为不做转置,称为梯度矩阵。
二阶偏导 #
标量函数的二阶梯度矩阵称为Hessian矩阵,先对标量函数求一阶梯度矩阵,然后求解Jacobian矩阵。
梯度流 #
梯度的负方向称为梯度流,即梯度下降的方向。
矩阵微分的计算 #
将标量矩阵函数转化为迹的形式,然后同时利用迹的性质和微分的性质。
| 性质 | 推论 | |
|---|---|---|
| $d(UV)=d(U)V+udV$ | $d(UVW)=d(U)VW+Ud(V)W+UVdW$ | |
| $d(AXB)=Ad(X)B$ | ||
| $d(X^TAX)=d(X)^TAX+X^TAdX$ | ||
| $d(tr(F(X)))=tr(d(F(X)))$ | $d(tr(X))=tr(d(X))$ | |
| $d(tr(X^TX))=2tr(X^TdX)$ | ||
| $d | X |
若矩阵微分$df(X)=tr(AdX)$,则雅可比矩阵$D_Xf(X)=\frac{f(X)}{\partial X^T}=A$,转置可得梯度矩阵$\nabla f(X)=\frac{f(X)}{\partial X}=A^T$,
常见函数的微分和梯度矩阵
| 函数 | 微分矩阵$df(X)=tr[\frac{\partial f(X)}{\partial dX}^TdX]$ | 梯度矩阵$\partial f(X)/\partial X$ | |
|---|---|---|---|
| $X$ | $I$ | ||
| $AX$ | $A^T$ | 注意迹可交换,因此$AX$和$XA$的梯度相同; 若$A$和$X$其一取转置,则梯度矩阵相应转置 |
|
| $X^2$ | $2X^T$ | ||
| $X^TX$ | $2X$ | ||
| $X^TAX$ | $(A+A^T)X$ | ||
| $XAX^T$ | $X(A+A^T)$ | ||
| $XAX$ | $X^TA^T+A^TX^T$ | ||
| $X^{-1}$ | $(X^{-2})^T$ | ||
| $AX^{-1}$ | $-(X^{-1}AX^{-1})^{T}$ |
共轭梯度 #
关于复变函数f(z),下列叙述等价
- f(z)是全纯/复解析函数
- f’(z)存在且连续
- f(z)满足Cauchy-Riemann方程
- f(z)的所有导数存在且拥有一个收敛的幂级数
虽然幂函数、指数函数、对数函数都是复解析函数,但存在一些常用函数不是全纯函数,例如$f(z)=z^*$和$f(z)=Re(z)$。
如果一个给定的复变函数可以写成$f(z)=f(z,z^)$的形式, 则可以直接求取其关于$z和z^$的偏导 。
无约束/带约束的优化问题 #
无约束优化 #
局部极小点的求解可以转化为 $$ f’(x)=0\newline f’’(x)>0 $$ 对于矩阵函数,即Jacobin矩阵为0且Hessian矩阵正定。
- 判断驻点是否为极大值,则判断$-f(x)$的驻点是否为极小值
- 既不是极大值、也不是极小值的驻点,称为鞍点
凸优化 #
| 线性规划 | 目标函数等高线是平行线 | 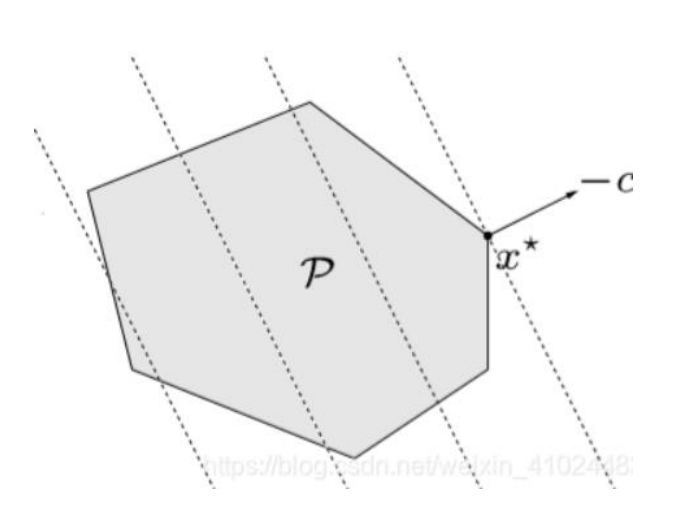 |
| 线性分式规划 | ||
| 二次规划 | 目标函数等高线是椭球面 | 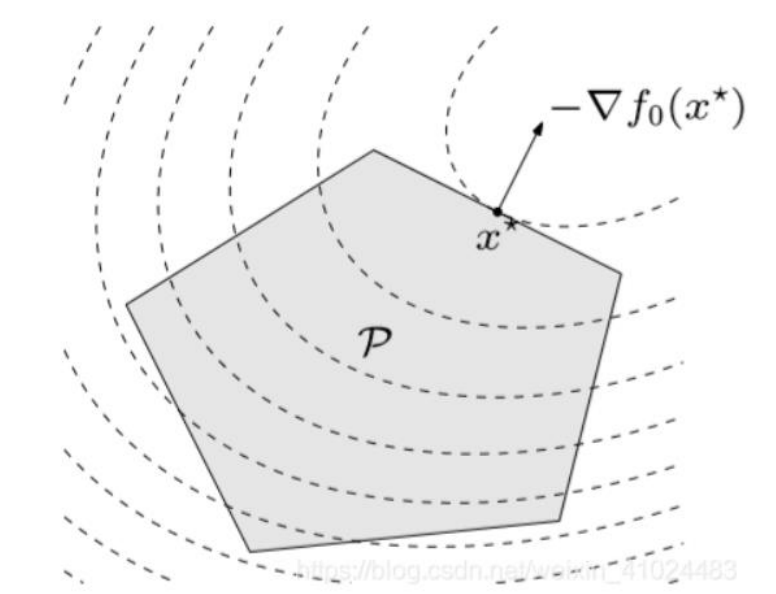 |
等式不等式约束的优化:拉格朗日乘子法 #
寻找“最好”(4)——不等约束和KKT条件 - 我是8位的 - 博客园 (cnblogs.com)
考虑某个带约束优化问题,含有等式约束和不等式约束 $$ \min_x f(x)\newline s.t.\quad h_i(x)=0\newline \quad g_i(x)\le0 $$ 联立模板函数和约束条件,有拉格朗日函数 $$ L(x,\lambda,\mu)=f(x)+\lambda h(x)+\mu g(x) $$
带约束优化问题的最优解必然满足KKT条件,即 $$ \begin{cases} \nabla_x L=0\newline h(x)=0\newline \lambda\ne0\newline \mu g(x)=0\quad互补松弛条件,不等式约束的极值,边界or无约束\newline g(x)\le0\quad原始不等式约束\newline \mu\ge0\quad对偶约束\newline \end{cases} $$ 满足KKT条件的解需要进一步检验,是否为最优
梯度下降法 #
略
矩阵分解 #
特征值和特征向量 #
若$Ax=\lambda x$,则称A存在特征值为$\lambda$的特征向量$x$
-
阶数为n的矩阵A有n个特征值,特征多项式的次数称为代数重数,特征值对应的特征向量空间的维度称为几何重数。
-
$A-\lambda I$的零空间维度,即$\lambda$对应的特征向量的维度
- 若$rank(A-\lambda I)\le n-1$,则$\lambda$为矩阵A的特征值
- $det(A-\lambda I)=0$是特征方程,可据此解得特征值$\lambda$
-
若矩阵$A$满足$\sum_{j}|a_{ij}<1|$,即每一行的和小于1,则$A$的每一个特征值的绝对值$|\lambda|<1$
考察矩阵A对向量x左乘变行,即每一行的线性组合,矩阵A的每一行是组合系数,而对于最大的元素,其它元素系数和为1的线性组合必然小于该元素,因此特征值必然小于1(不等式放缩)
若矩阵$A$的特征值为$\lambda$,则它的不同运算结果的特征值如下:
| 矩阵 | 特征值 | |
|---|---|---|
| $A^T,P^{-1}AP$ | ${\lambda}$ | 转置和相似不改变$A-\lambda I$的秩 |
| $A^k$ | ${\lambda}^k$ | |
| $A^{-1}$ | $1/\lambda$ | |
| $A+\sigma^2I$ | $\lambda+\sigma^2$ |
- $AA^H$的特征值可通过在$Ax=\lambda x$方程两边同乘以$A$的方式,构造出$AA^H$对特征向量$Ax$的特征值。
某些特殊矩阵的特征值如下:
| 矩阵 | 特征值 |
|---|---|
| 幂等矩阵 | 0或1 |
| 实正交矩阵 | 1或-1 |
| 单位阵 | 1 |
| 全1阵 | 对全1向量的特征值为N,其他特征值全为0 |
特征值与迹、行列式、秩的关系 #
| 推论 | ||
|---|---|---|
| 迹 | 特征值之和 | |
| 行列式 | 特征值之积 | |
| 秩 | 非零特征值的个数 | 若矩阵A存在一个单重特征值0,则秩为n-1 |
广义特征值 #
若$Ax=\lambda Bx$则称$\lambda,x$是矩阵束$A,B$的广义特征值和特征向量
矩阵束左乘/右乘非奇异矩阵,不会改变广义特征值和特征向量
特征值分解(EVD) #
若$A$有**$n$个线性无关的特征向量**,则有$AU=U\Sigma$,其中$U$是特征向量构成的矩阵,因为$U$满秩,所以$U$可逆,有特征值分解$A=U\Sigma U^{-1}$
特别地,矩阵$A$可酉对角化的充要条件是$A$是正规矩阵,即$A^HA=A^HA$,有$A=U\Lambda U^H$
- 对称阵(实对称阵、Hermitian阵)、正定阵可以酉对角化
- 正定阵的特征值>0
奇异值分解(SVD) #
任意矩阵$A$可以奇异值分解为$A=U\Sigma V^H$,其中$U$的列向量是$AA^H$的特征向量,$V$的列向量是$A^HA$的特征向量,对角线上是矩阵$A$的奇异值,是$AA^H$和$A^HA$的特征值的非负平方根,通常由大到小排列
- 由$AV=U\Sigma$可知$A\overrightarrow{v_i}=\sigma_i\overrightarrow{u_i}$,奇异值的个数取决于其中维数小的矩阵
- 由矩阵乘法的秩1分解视角,$A=\sum_i \lambda_iu_iv_i^H$,其中$\lambda_i$是非零奇异值
- 若矩阵可EVD,则奇异值和特征值等价
- SVD生动动画演示:旋转-拉伸-升降维度-旋转
SVD vs EVD #
| SVD | EVD |
|---|---|
| 适用于任何$m\times n$矩阵 | 只适用于$n\times n$方阵 |
| 奇异值与奇异向量的关系 $u_i^HAv_i=\sigma_i$ |
特征值与特征向量的关系 $Av_i=\lambda_iv_i$ |
A的非零奇异值是$A^HA$或$AA^H$的非零特征值的正平方根;
A的左奇异向量是$AA^H$的特征向量;A的右奇异向量是$A^HA$的特征向量;
Jordan标准形 #
任一方阵可块对角化为Jordan标准型,即$J=P^{-1}AP$
其中$J=\begin{bmatrix} J_1(\lambda_1)\quad \quad \newline \quad J_2(\lambda_2) \quad \newline \quad \quad J_3(\lambda_3)\end{bmatrix}$,而$J_i(\lambda_i)=\begin{bmatrix} \lambda_i\quad1\quad0\newline 0\quad \lambda_i \quad1\newline 0\quad 0\quad \lambda_i\end{bmatrix}$
特征分析 #
Cayley–Hamilton定理 #
将矩阵$A$代入其特征多项式$f(\lambda)=0$,即为矩阵$A$的零化多项式
-
根据多项式除法,任意矩阵幂可以由矩阵的零次幂到N-1次幂线性组合得到,线性系数可以通过n个特征值的线性方程组联立得到
-
逆矩阵的计算
-
矩阵微分方程的求解
Rayleigh商 #
瑞利商$R(A,x)=\frac{x^TAx}{x^Tx}$
为了简化问题令$X^xx=1$,求$x^TAx$的条件极值
构造拉格朗日乘子函数$L(x,\lambda)=x^tAx+\lambda(x^Tx-1)$,对$x$求梯度,令梯度为0,解得极值点$Ax=\lambda x$
显然,在最大的特征值对应的特征向量处,瑞利商有最大值;在最小的特征值对应的特征向量处,瑞利商有最小值
根据瑞利商的性质,结合放缩,可推导出以下结论:
| 取等 | |
|---|---|
| $\lambda_1(A+B)\ge\lambda_1(A)+\lambda_N(B)$ | $A$的最大特征向量是$B$的最小特征向量 |
| $\lambda_N(A+B)\ge\lambda_N(A)+\lambda_N(B)$ | $A,B$最小特征向量相同 |
| $\lambda_1(A+B)\le\lambda_1(A)+\lambda_1(B)$ | $A,B$最大特征向量相同 |
广义瑞利商 #
考虑广义特征值$Ax=\lambda Bx$,则有广义瑞利商$R(A,B,x)=\frac{x^TAx}{x^TBx}$,可以进一步转化为$B^{-1}A$的瑞利商
线性方程 #
线性方程组$AX=b$的解 #
假设线性方程组$AX=b$有m个方程、n个未知数,即系数矩阵$A\in C^{m\times n}$,则解的情况为:
| 独立方程个数 | 增广矩阵和系数矩阵的关系 | 系数矩阵 | 线性空间 | |
|---|---|---|---|---|
| 有唯一解 | 适定方程 | $r(A|b)=r(A)$ | $r(A)=m=n$ | $b\in Col(A)$ |
| 有无穷多解 | 欠定方程 | $r(A|b)=r(A)$ | $b\in Col(A)$ | |
| 无解 | 超定方程 | $r(A|b)>r(A)$ | $b\notin Col(A)$ |
最小二乘 #
对于超定方程,可使用最小二乘法求取近似解
| 代价函数 | 优化视角 | 投影视角 | |
|---|---|---|---|
| 普通最小二乘 | $(Ax-b)^T(Ax-b)$ | 认为观测量$b$含噪,最小化$e$ | 考察方程$Ax=b$的近似解,即$b$在$A$的列空间的投影$p=Pb=A\hat{x}$,投影$p$是$A$的列向量的线性组合$b$去除投影分量后与$A$的列空间垂直,即$A^T(A\hat{x}-b)=0$,解得$A\hat{x}=A(A^TA)^{-1}A^Tb$投影矩阵$P=A(A^TA)^{-1}A^T$满足最小二乘的近似解$\hat{x}=(A^TA)^{-1}A^Tb$ |
| 数据最小二乘 | $\frac{(Ax-b)^T(Ax-b)}{x^Tx}$ | 认为原始数据$A$含噪,最小化$E$ | |
| 总体最小二乘 | $\frac{\begin{bmatrix}x\newline-1\end{bmatrix}^T[A,b]^T[A,b]\begin{bmatrix}x\newline-1\end{bmatrix}}{1+x^Tx}$ | 认为总体含噪,即$(A+E)x=b+e$,最小化$[E,e]$的二范数 设增广数据矩阵为$A$,则总体最小二乘的解向量是$A$最小的奇异值对应的右奇异向量,或者$A^TA$的最小特征值对应的特征向量 |
线性空间 #
在集合$V$和数域$K$上定义加法和数乘运算,若满足8条基本性质,则称集合$V$是$K$上的线性空间
- 如果没有定义新的加法和数乘,则只需满足对加法和数乘封闭
- 线性变换:满足线性性质,即齐次性和可加性
维数 #
线性空间中向量构成的极大无关组的向量个数是该空间的维数
维数公式:$dim(S_1+S_2)=dim(S_1)+dim(S_2)-dim(S_1 \cap S_2)$
- 和空间的维数可以求解矩阵的秩,基向量可以消去任意若干直至等于秩
- 交空间的维数可以用维数公式,基向量的求解方式为:将交空间的向量用两个空间的向量分别表示,得到线性方程组,将交空间的向量用某一个空间的系数和基向量表示出来,再合并系数即可。
子空间 #
线性空间的子集,若封闭,则称为子空间,即$\forall v_1,v_2 \in V, \exists \lambda_1,\lambda_2, \lambda_1v_1+\lambda_2v_2 \in V$
列空间、行空间、零空间 #
设矩阵$A\in R^{M\times N}$,则相应地有下列子空间:
| 子空间 | 维度 | 原空间 | 等价 | |
|---|---|---|---|---|
| 列空间 | $Col(A)$ | $R^m$ | $R^M$ | $Row(A^H)$ |
| 行空间 | $Row(A)$ | $R^n$ | $R^N$ | $Col(A^H)$ |
| 零空间 | $Null(A)$ | $R^n$ | $AX=0$的解空间 | |
| $Null(A^H)$ | $R^m$ |
-
若矩阵是非奇异的,则说明$Ax=0$的解空间是零向量空间(只有零解)
-
N维实数空间$R^N$可以分解为矩阵的列空间和零空间的直和,即$R^N=Col(A)\oplus Null(A)$
-
直和:无交子空间的和
证明两个子空间的和是直和(无交)
首先计算两个子空间的和,计算极大无关组的秩,得到和空间的维数,然后根据维数公式计算交空间的维数(为0),证明无交,即为直和
不变子空间 #
若$Ax=\lambda x$的特征向量张成的子空间称为矩阵$A$的不变子空间,即对A封闭
投影矩阵 #
投影矩阵必定是幂等矩阵,有$A^2=A$,特征值为0和1,相当于只保留若干个方向的分量,其余方向的分量置零
但是,投影矩阵未必一定是正交投影,特征值为1的特征向量实际上有无穷多个,然而只有一个和投影方向是正交的
投影矩阵是正交投影矩阵,当且仅当它是对称幂等矩阵