Medical Image Computing

Table of Contents

CT Reconstruction
#

Analytical CT reconstruction
#

Radon Transform

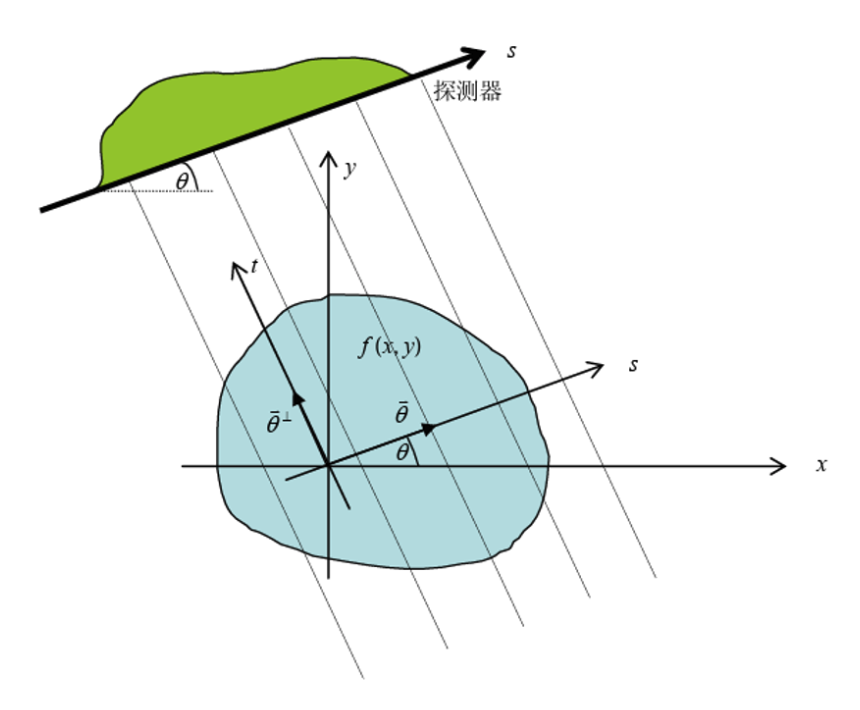
数学形式化描述

$$ p(s,\theta)=\int^\infty_{-\infty}\int^\infty_{-\infty}f(x,y)\delta(xcos\theta+ysin\theta-s)dxdy $$

$s,\theta$确定时，相当于仅在直线$xcos\theta+ysin\theta-s=$上作积分

代码实现

from skimage.transform import warp

theta = np.arange(180)
# pad
padded_image = np.pad(image, pad_width, mode='constant',
                      constant_values=0)
center = padded_image.shape[0] // 2
# 旋转+投影
radon_image = np.zeros((padded_image.shape[0], len(theta)),
                       dtype=image.dtype)
for i, angle in enumerate(np.deg2rad(theta)):
    cos_a, sin_a = np.cos(angle), np.sin(angle)
    R = np.array([[cos_a, sin_a, -center * (cos_a + sin_a - 1)],
                  [-sin_a, cos_a, -center * (cos_a - sin_a - 1)],
                  [0, 0, 1]])
    rotated = warp(padded_image, R, clip=False)
    radon_image[:, i] = rotated.sum(0)

Sinogram

正弦图的每一个$\theta$都对应一组s轴上的投影

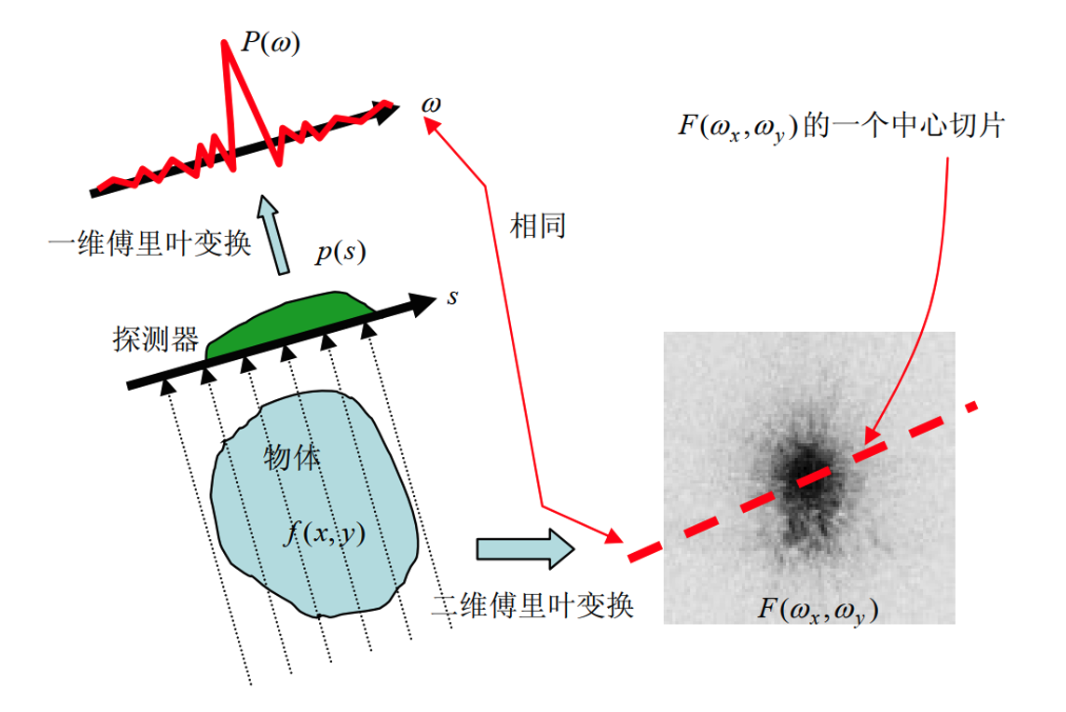
中心切片定理

二维图像的中心切片定理指出：二维函数 f(x, y) 的投影 p(s) 的傅里叶变换 P(ω) 等于函数 f(x, y) 的傅里叶变换 F(ωx,ωy) 沿与探测器平行的方向过原点的片段。

FilteredBackProjection (FBP)

证明：

数学形式化描述

$$f(x,y)=\int^\pi_0q(s,\theta)|_{s=x\cos\theta+y\sin\theta}d\theta$$

代码实现

reconstructed = np.zeros((output_size, output_size),dtype=dtype)
radius = output_size // 2
xpr, ypr = np.mgrid[:output_size, :output_size] - radius
for col, angle in zip(radon_filtered.T, np.deg2rad(theta)):
    t = ypr * np.cos(angle) - xpr * np.sin(angle)
    reconstructed += interpolant(t)
reconstructed = reconstructed* np.pi / (2 * angles_count)

MRI Reconstruction
#

Image Enhancement & Restoration
#

Image Quality Assessment
#

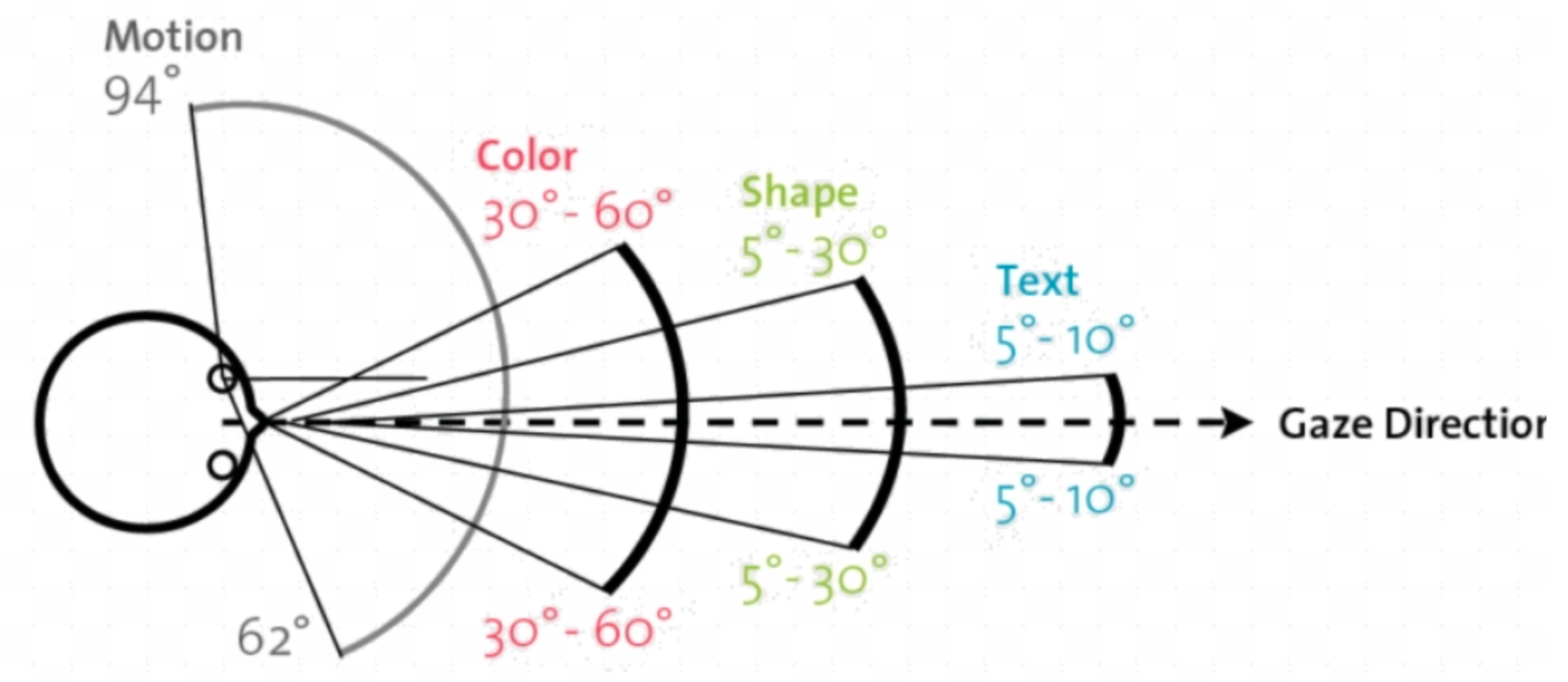
Human visual system (HVS)

视敏度	visual acuity	20/20 is ~1 arc minExtreme acuity = 0.4 arc min =1/150 of a degree
视野	field of view	~190° monocular, ~120° binocular, ~135° vertical
空间分辨率	spatial resolution	~576 megapixels
时间分辨率	temporal resolution	~60 Hz
动态范围	dynamic range
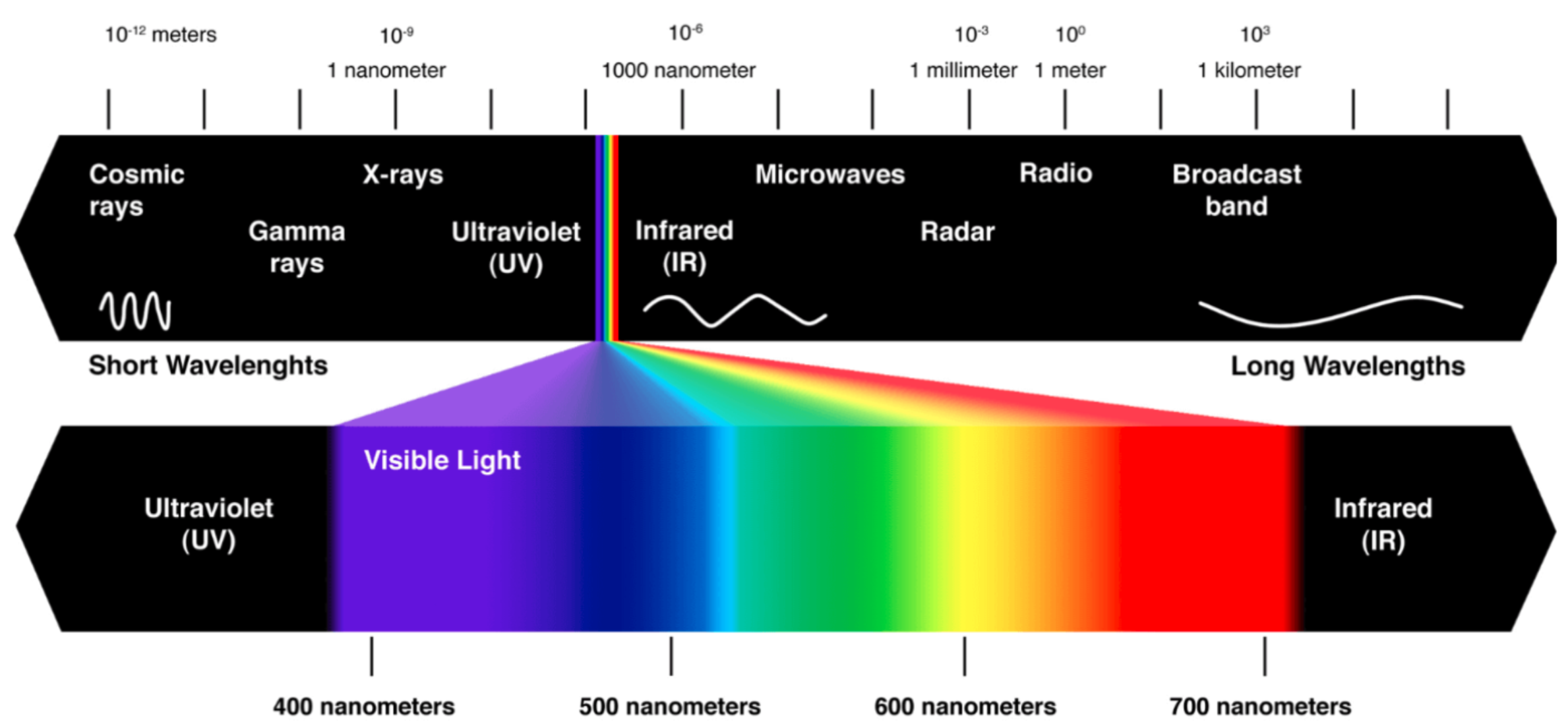
颜色	color
深度	depth cues in 3D displays
聚焦范围	accommodation range	~8cm to ∞, degrades with age

Image Quality Metric

Signal-to-Nosie Ratio (SNR)	Is SNR a good metric? Nope!

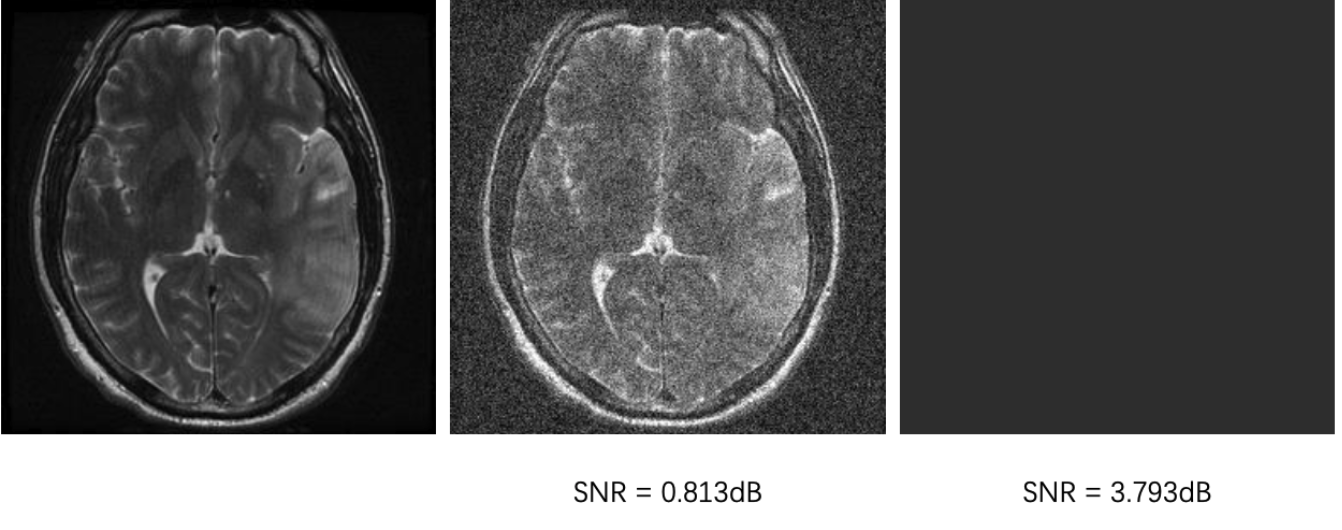
Structural similarity index measure (SSIM)	$$ssim(x, y)={l(x, y)}^{\alpha} {c(x, y)}^{\beta} {s(x, y)}^{\gamma}$$
	$$luminance\ l(x, y)=\frac{2\mu_x\mu_y+c_1}{\mu_x^2+\mu_y^2+c_1}$$$$contrast\ c(x, y)=\frac{2\sigma_x\sigma_y+c_2}{\sigma_x^2+\sigma_y^2+c_2}$$$$structure\ s(x, y)=\frac{2\sigma_{xy}+c_3}{\sigma_x\sigma_y+c_3}$$


Multi-scale SSIM

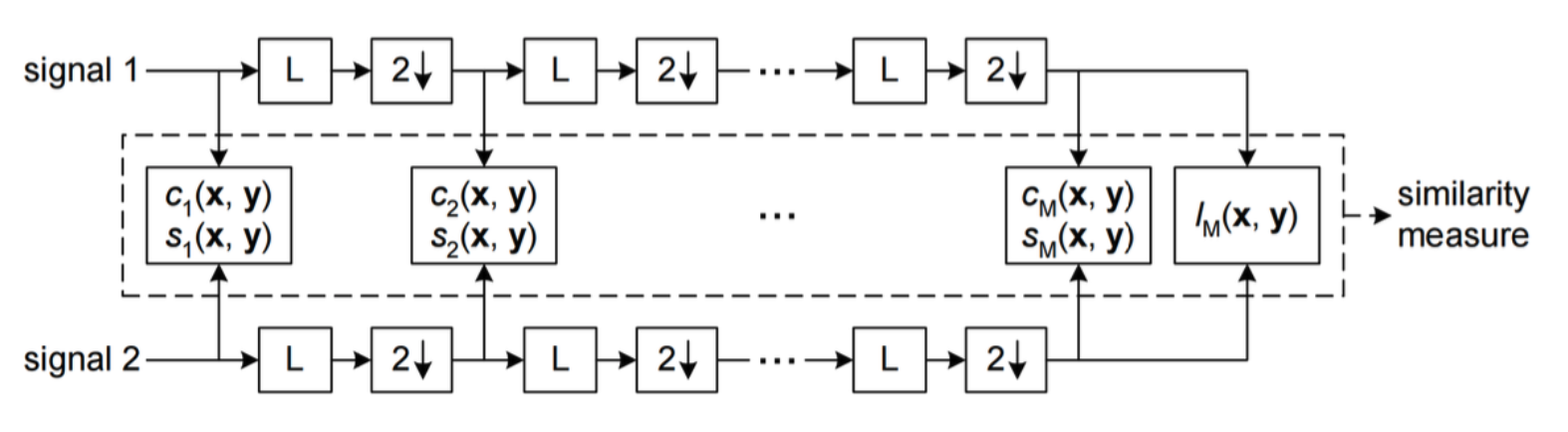
No-reference image quality assessment (NR-IQA)

Blind/Reference-less Image Spatial Quality Evaluator (BRISQUE)
Naturalness Image Quality Evaluator (NIQE)
Perception-based Image Quality Evaluator (PIQE)

Image Enhancement
#

Global (or spatially uniform) operators

Reinhard	$$I_{out}=\frac{I_{in}}{I_{in} + 1}$$
Gamma compression	$$I_{out}=AI_{in}^\gamma$$
Look-up table (LUT)
Histogram equalization	寻找$$s=T(r)$$使得$$f(s)=f(r)\frac{dr}{ds}=\frac{1}{L-1}$$，易得$$\frac{ds}{dr}=f(r)(L-1)$$，积分可得$$s=\int_0^r{f(r)(L-1)dr}$$

Local (or spatially varying) operators

Unsharp masking	$$I_{out}=I_{in}+\lambda Z$$$$Z=HF(I_{in})=I_{in}-LF(I_{in})$$	增强低频/高频分量
Guassian/Bilateral/… Filtering

Gradient domain tone mapping

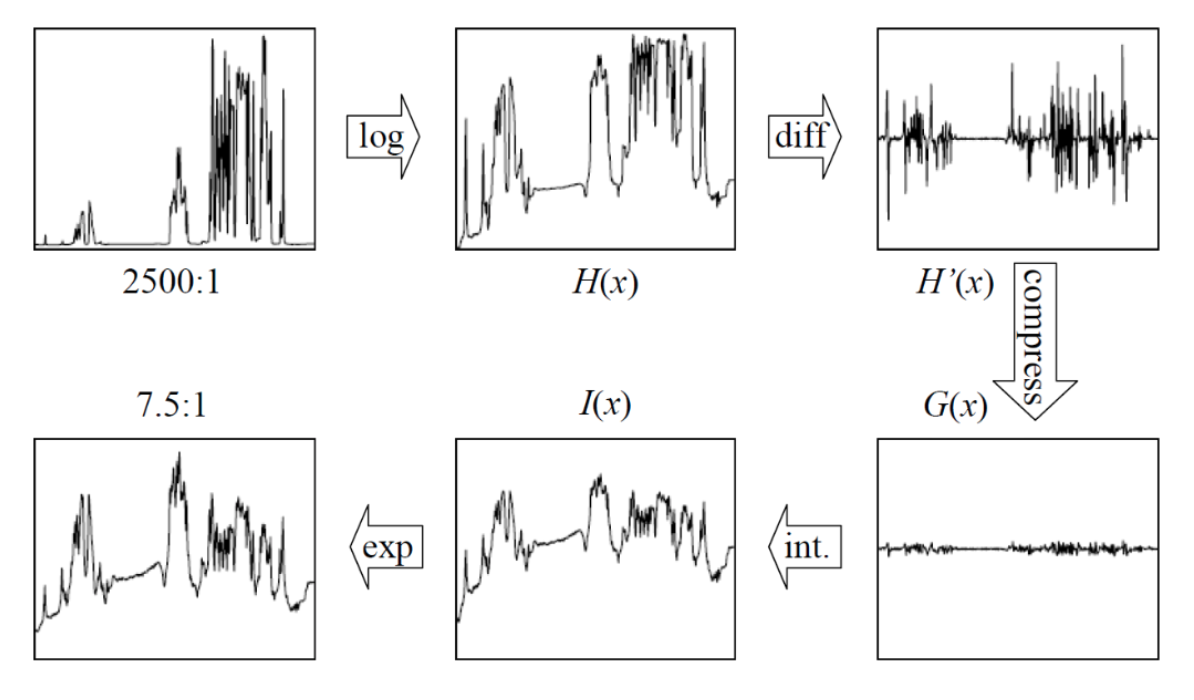
Multiscale tone-mapping

Image Restoration
#

Imaging model

Noise	Expression	Solution
Blur（Multiplicative）	$$Y=AX$$	Deblur
Downsample	$$Y=\downarrow_r X$$	Superresolution
Mask	$$Y=X(1-M)+ZM$$	Inpainting
Noise (Addictive)	$$Y=AX+N$$	Denoise

Direct method: function approximation

Mean filter	Assumptions: 噪声和信号独立，噪声相互独立$$E(\overline{N}^2)=\frac{1}{n}\sigma^2$$ $$ SNR_{avg} = nSNR_{orig}$$
Gaussian filter	$$f(p)=\frac{1}{\Sigma_{p\in\Omega} f(p-s)}\Sigma_{p\in\Omega} f(p-s)I_p$$	距离越近，权重越大
Edge-preserving filter	三大保边滤波，防止边缘因滤波而模糊
Bilateral filter (BF)	$$f(p)=\frac{1}{\Sigma_{p\in\Omega} f(p-s)g(I_p-I_s)}\Sigma_{p\in\Omega} f(p-s)g(I_p-I_s)I_p$$	距离越近，像素值越接近，权重越大
Guided filter (GF)	$$O_i=\overline{a_k}G_i+\overline{b_k}$$其中$$a_k=\frac{Cov_{W_k}(G,I)}{Var_{W_k}(G)+\epsilon}$$, $$b_k=E_{W_k}(I)-a_kE_{W_k}(G)$$	物理意义等等再写
Weighted least squares filter(WLSF)
Nonlocal Means	在全局范围内计算权重
Block-matching and 3D filter (BM3D)	Block-matching: 寻找相似的图像块3D Filter: 在堆叠的图像块上进行3D滤波Aggregation: 3D->2D

Implicit method: A probabilistic framework for denoising

由$$Y=AX+$$可得$$Y-AX=N$$，进一步有$$f(Y|X)=f(N)$$

假定噪声服从高斯/拉普拉斯/泊松分布，则获得了$$f(Y|X)$$的含参数表达式

使用极大似然估计，可以得到参数的估计值

$${argmax}{\sigma, X} P(Y|X)={argmin}{\sigma, X} -logP(Y|X)$$

假定噪声服从Gaussian分布，则有$$X=argmin_{X}|Y-AX|^2/2\sigma^2$$

假定噪声服从Laplacian分布，则有$$X=argmin_{X}|Y-AX|/2\sigma$$

Bayesian/optimization approach

$$max_X P(X|Y)=P(Y|X)P(X)/P(Y)$$

$$min_X L(X)=|Y-AX|^2/2\sigma^2+\lambda R(X)$$

R(X)是X的正则项/反转分布，取决于对X的先验

Image prior: Sparsity presentation

Dictionary learning: to find D

Sparse coding

$$min_{\alpha} |\alpha|_0\ subject\ to\ x=D\alpha$$

Denoising (given D)

$$min_\alpha |\alpha|_0{\ subject \ to}|x-D\alpha|_2<\varepsilon$$

Which dictionary to use?

Choose D from a known set of transforms

Eg. Fourier Transform/Cosine Transform/Steerable wavelet/Curvelet/Contourlets/Bandlets/Shearlets

Learn D from a set of examples

Such learning should sparsify the representation as much as possible.

Image Segmentation
#

Distance

Connection

Polar

中心扩散/梯度

根据物体的形状/…特点寻找合适的表达

Threshold: m(x,y)=F(I(x,y))>t

Water

Region growing

cluster

CT Reconstruction #

Analytical CT reconstruction #

MRI Reconstruction #

Image Enhancement & Restoration #

Image Quality Assessment #

Image Enhancement #

Image Restoration #

Image Segmentation #