相似性度量 #
最小距离分类器 #
将样本归入距离最近的类别
| 平均样本法 | 样本到每个类别的各样本平均值的距离 |
| 平均距离法 | 样本到每个类别的各个样本的距离的平均值 |
| 最近邻法 | 样本最近的样本 |
距离,即相似性测度,常用的测度有:欧式距离、马氏距离($(X-M)^T\Sigma(X-M)$,衡量了样本到分布的距离)、向量夹角余弦
线性分类器 #
n维线性分类器可以表达为超平面$w^Tx+b=0$ 如果将样本X的第n+1维设为1,则超平面可以简化为$w^Tx=0$ 若样本集线性可分,则存在分类器使得所有样本满足$\begin{cases}w^Tx>0\quad if\ x\in w_1\newline w^Tx<0\quad if\ x\in w_2\end{cases}$
线性分类器的解必然构成解区域,解是不确定的
多分类问题按照是否线性可分、是否存在不确定区域的解可以分成三种情况
| 情况 | 分类器 | |
|---|---|---|
| 总体线性可分 | 训练n个超平面,分隔每个类和其他所有类 | |
| 成对线性可分 | 用$C_n^2$个独立的超平面,将两个类别分开 | |
| 成对线性可分,且存在没有不确定区域的解 | 每个类别训练一个判别函数,采用最大值判决 $G_{ij}(X)=g_i(X)-g_j(X)$ |
感知器 #
线性分类器+阶跃函数
按顺序遍历样本,直到所有样本被正确分类
若样本$X_i$满足$\begin{cases}W^TX_i>0\quad if X_i\in\omega_1\newline W^TX<0\quad if X_i\in\omega_2\end{cases}$,则说明该样本被正确分类;
否则:$W=\begin{cases}W+\rho X_i\quad if X_i\in\omega_1\newline W-\rho X_i\quad if X_i\in\omega_2\end{cases}$
学习率和优化器 #
学习速率$\rho$有很多设定方法,例如固定值、绝对修正(保证当前的单个训练样本被修正)、部分修正(对绝对修正的速率取0-2之间的调节因子)、变速学习(例如先快后满)、优化学习(令每一步最优,但计算量大)等。
常用的梯度下降法有:批量梯度法(BGD)、随机梯度法(SGD)、小批次梯度法(MBGD),分别对应整个数据集、单个样本、一小批样本进行梯度的计算。
最小平方和,LMSE #
如果引入松弛变量,给每个样本的判别函数值规定一个数值,那么n个样本相当于添加了n个约束(具体取决于秩),当n>样本维度时,这是一个超定方程,只能转化为最优化问题来求解。
如果使用最小均方误差(Least Mean Square Error, LMSE)来求解,准则函数为 $$ J(w)=||Xw-b||^2 $$ 相应的梯度为 $$ \nabla J(w)=\nabla ||Xw-b||^2 = 2X^T(Xw-b) $$ 相应的更新方式为 $$ w_{k+1}=w_k+\rho_{k+1}X^T(Xw+b) $$ 但是,上述方法需要给定松弛变量,事实上,松弛变量也可以在优化中求解,即H-K算法。 $$ b_{k+1}=b_k-\eta_{k+1}\nabla J(w(k))|b $$
$$ \nabla J(w(k))|_b = -2(Xw(k)-b) = -2e(k) $$
$$ b_{k+1}=b_k+2\eta_{k+1}e_k $$
为保证b>0,使其单调递增, $$ b_{k+1}=b_k+\eta_{k+1}(e_k+|e_k|) $$
而对于w,直接令偏导数为0, $$ \nabla J(w(k))|_w = 2X^T(Xw-b)=0 $$
解得 $$ w_{k+1}=(X^TX)^{-1}X^Tb_{k+1} =w_k+\eta_{k+1}(X^TX)^{-1}X^T|e_k| $$
若训练集线性可分,则误差向量e可以优化至0;反之,当误差向量<0,说明样本集线性不可分。
SVM #
寻找一个最优分类超平面,到两类中最靠近的样本点的距离同时达到最大
边界上的样本点称为支持向量,支持向量到超平面的距离可通过点到直线的距离公式求得, $$ r = \frac{G(x)}{||w||} $$ 进而有优化式 $$ \max d = \max 2r = \max \frac{2|G_{ij}(x_s)|}{||w||} $$ 由于直线的系数w可以等比例地放大或缩小,不妨令分子为1,则有 $$ \min||w|| $$ 等价于 $$ \min \frac{1}{2}||w||^2 $$ 支持向量是距离超平面最近的点,其他向量到超平面的距离必须更大,则有不等式 $$ G_{ij}(x)=w^Tx_i+w_0\ge1\newline 或者\newline G_{ij}(x)=w^Tx_i+w_0\le-1 $$ 合并为 $$ sgn(G_{ij}(x_i))(w^Tx_i+w0)\ge1 $$
使用拉格朗日乘子法,不等式约束可转化为 $$ \min_{||w||}\max_{\alpha}L(w,w_0,\alpha)=\frac{1}{2}||w||^2-\sum_i^l \alpha_isgn(G_{ij}(x_i))(w^Tx_i+w_0-1) $$ 最优化问题的解必满足KKT条件 $$ \begin{cases} \alpha_i\ge0\newline sgn(G_{ij}(x_i))(w^Tx_i+w0)\ge1\newline \sum\alpha_isgn(G_{ij}(x_i))(w^Tx_i+w0-1)=0 \end{cases} $$ 权向量是支持向量的线性组合 $$ w=\sum_i sgn(G_{ij}(x_i))\alpha_ix_i $$ 偏置量$w_0$可代入任意一个支持向量求得。
Fisher线性判别,LDA #
将样本点投影到一条直线上,使得投影后的类间距离尽可能大,类内距离尽可能小。
类内离散度矩阵$S_i=\sum_{x_k\in w_i} (x_k-\mu_i)(x_k-\mu_i)^T$,它刻画了样本偏离均值的差异程度;总的类内离散度矩阵$S_w=\sum_i S_i$,它刻画了两类样本偏离各自均值的总的差异程度
当样本数足够多时,$S_w$非奇异,最优投影直线的方向存在解析解$w^*=S_w^{-1}(m_1-m_2)$
非线性分类器 #
势函数法 #
定义位势函数$K(X)=\sum \lambda_iK(X,X_i)$,使得正样本的位势>0,负样本的位势<0
其中$K(X,X_i)$是单个样本点的位势,在样本点处有极大值,单调递减,在无穷处趋于0
位势函数本质上是样本点位势的加权和,但每个样本点的权重是不同的,需要在迭代中更新
按顺序遍历样本,直到所有样本满足:正样本的位势>0,负样本的位势<0
若样本$X_i$满足$\begin{cases}K_A(X_i)>0\quad if X_i\in\omega_1\newline K_A(X_i)<0\quad if X_i\in\omega_2\end{cases}$,则$K_A(X)$不变;
否则:$K_A=\begin{cases}K_A(X)+K(X,X_i)\quad if X_i\in\omega_1\newline K_A(X)-K(X,X_i)\quad if X_i\in\omega_2\end{cases}$
非线性SVM #
软间隔:对于异常点,设置松弛变量,允许异常点在一定程度内的存在,以防止无解
核函数:将样本点映射到高维空间,进行线性可分的求解
贝叶斯分类器 #
$P(w_i)$先验概率:类别的先验
$P(x|w_i)$类条件概率:每个类别内样本的分布
根据先验概率和类条件概率,可以计算后验概率 $$ P(w_i|x)=\frac{P(x|w_i)P(w_i)}{\sum_j P(x|w_j)P(w_j)} $$
贝叶斯判别器 #
| 判别准则 | ||
|---|---|---|
| 最大后验概率/最小错误概率判决 | $g_i(X)=P(\omega_i|X)$ | 概率越大,值越大 |
| 最小风险判决 | $g_i(X)=-R(\alpha_i|X)=-\sum_i R(\alpha_i|w_i)$ | 风险越小,值越大(风险:误判成其它类的风险之和) |
| Neyman-Pearson判决 | 调整判决阈值,使一类错误率不变。另一类错误率减小,可使用拉格朗日方法求解 | |
| 最小最大判决 | 使风险最大的判决可能性最小(保守,最坏情况下结果最好,其他情况下结果可用) |
最小错误概率本质上是最小风险的在正确风险为0、错误风险为1的一种特例
类条件概率密度的估计 #
参数估计 #
如果知道类间概率服从何种分布,则可以估计相应的分布参数。
| 极大似然估计 | $\max_\theta P(X|\theta)$, 其中第i类样本的似然函数$p(X_i|\theta_i)=\prod_k^Np(x_k|\theta_i)$ |
调整$\theta$,使取得样本集$X$的概率最大 |
| 贝叶斯估计 | 设待估参数的先验概率为$P(\theta_i)$,则后验概率为$p(\theta_i|X_i)=\frac{p(X_i|\theta_i)P(\theta_i)}{\int_{\theta_i}p(X_i|\theta_i)P(\theta_i)d\theta}$ | 利用贝叶斯公式,根据样本集的概率分布,反推参数$\theta$的后验概率,然后计算$\theta$的数学期望 |
朴素贝叶斯认为样本的各个维度独立,故似然概率可以表达为 $$ P(x|w)=\prod_j P(x_j|w) $$
非参数估计 #
包括Parzen窗估计法和k近邻估计法。
聚类 #
聚类定义:不知道每个类别的具体分布
聚类准则:类间距离大,类内距离小
| 离散度矩阵 | ||
|---|---|---|
| 类内离散度矩阵 | $S_j=\frac{1}{N_j}\sum_{x_k\in w_j} (x_k-m_j)(x_k-m_j)^T$ | |
| 总的类内离散度矩阵 | $S_w=\sum_j P_j S_j$ | within |
| 类间离散度矩阵 | $S_b=\sum_j P_j(m_j-m)(m_j-m)^T$ | between |
| 总的离散度矩阵 | $S_t=\frac{1}{N}\sum_k (x_k-m)(x_k-m)^T$ | total |
三个离散度矩阵满足$S_t=S_w+S_b$
| 聚类准则函数 | ||
|---|---|---|
| 误差平方和 | $J_e=\sum_j^C \sum_i^{N_j} ||x-m_j||^2$ | |
| 加权平方和 | $J_l=\sum_j^C P_jD_j$其中$D_j=E(||x-m_j||^2)$ |
增类聚类:最大最小距离 #
最大最小距离:先计算每个点到最近的聚类中心的距离(最小),然后选择其中距离最远的点(最大)
先指定一个聚类中心,相距最远的作为另一个聚类中心
不断迭代,增加新的聚类中心,直至样本点的最大最小距离<阈值
减类聚类:层次聚类 #
不断合并距离最近的两个类,第K次合并时的类别数$C=N-K+1$
初始情况,每个样本各成一类;
计算类间距离,合并距离最小的两个类;(新的类间距离取决于类内样本的均值)
继续合并类,直至类间距离大于阈值或者类别数k满足要求;
动态聚类:C均值聚类(k-means) #
优化准则函数$J_e$,使得类内误差平方和最小
设定k个聚类中心
每个样本进行分类,使得类内误差平方和最小(实际就是KNN),从而更新聚类中心
不断地迭代(分类+更新中心),直至聚类中心不再被更新
-
初始聚类中心和类别数会影响收敛速度和边界样本的类别归属(但总是收敛的)
-
可以选择几何意义明确的点作为聚类中心。
-
准则函数实质上是MSE,可以选择MSE曲线的拐点作为最佳类别数k。
近邻函数聚类 #
近邻函数:每个样本点到其他样本点的距离
计算距离矩阵D
计算近邻系数矩阵$M=[m_{ij}]$,$X_i$是$X_j$的第$m_{ij}$个近邻
计算近邻函数值矩阵$A=[a_{ij}],a_{ij}=\begin{cases}m_{ij}+m_{ji}-2,i\ne j\newline2N,i=j\end{cases}$
找出每行的最小元素,将距离最近的样本点连起来,形成初始聚类
对于每个类别,寻找与之距离最近的类别,若类间距离(min)<类内距离(max,min),则合并两个类别;不断迭代,直至无法合并
最小生成树聚类 #
先构建出最小生成树
然后找到权值最大的一条边,将样本集分为两个子集,递归地进行,直至最大边小于阈值
| 最小生成树算法 | 适用 | |
|---|---|---|
| Prim | 先找到最小边,然后依次向外扩展最小的边,且不能构成环路,直至连通 | 节点少 |
| Kruskal | 依次寻找最小的边,且不能构成环路,直至连通 | 边少 |
句法分析 #
文法:根据一定规则产生样本
| 类型 | 符号 | |
|---|---|---|
| 终止符 | $V_T$$V_T=\set{a,b,c}$ | Terminal |
| 非终止符 | $V_N=\set{S,A,B,C}$ | Nonterminal |
| 起始符 | $S$,一类特殊的非终止符 | |
| 产生式 | $\alpha\rightarrow\beta,\alpha\in V^+,\beta \in V^*$ | Parse |
4种基本文法与自动机 #
| 类型 | 文法 | 限制 | |||
|---|---|---|---|---|---|
| 0型文法 | 无约束文法 | $\alpha\rightarrow\beta$ | 无 | 递归特性,可以产生一切类型的样本 | 图灵机 |
| 1型文法 | 上下文有关 | $\alpha_1A\alpha_2\rightarrow\alpha_1B\alpha_2$ | 考虑上下文,但上下文也可以为空 单个非终止符 |
上下文也可以是空句 | 线性界限自动机 |
| 2型文法 | 上下文无关 | $A\rightarrow\beta$ | 单个非终止符 | 最左推导/最右推导(从最左/最优的非终止符开始推导) | 下推自动机 |
| 3型文法 | 正则 | $A\rightarrow a$ $A\rightarrow aB$ |
左:单个非终止符 右:单个终止符/单个终止符+单个非终止符 |
可以用状态图表示 | 有限状态自动机 |
4种文法的关系:限制逐渐增加,范围逐渐缩小
句法识别 #
句法识别方法:样本是否能被模式类的文法生成
$模式类\omega_i对应的文法是G_i,如果x\in L(G_i),那么则判定x\in w_i$
| 参考匹配法 | 每个模式类根据对应的文法生成对应的参考列,将样本与每一列的参考列逐个比对 | |
| 状态图法 | 对于正则文法,若能找到状态图中的通路,则属于模式类 | 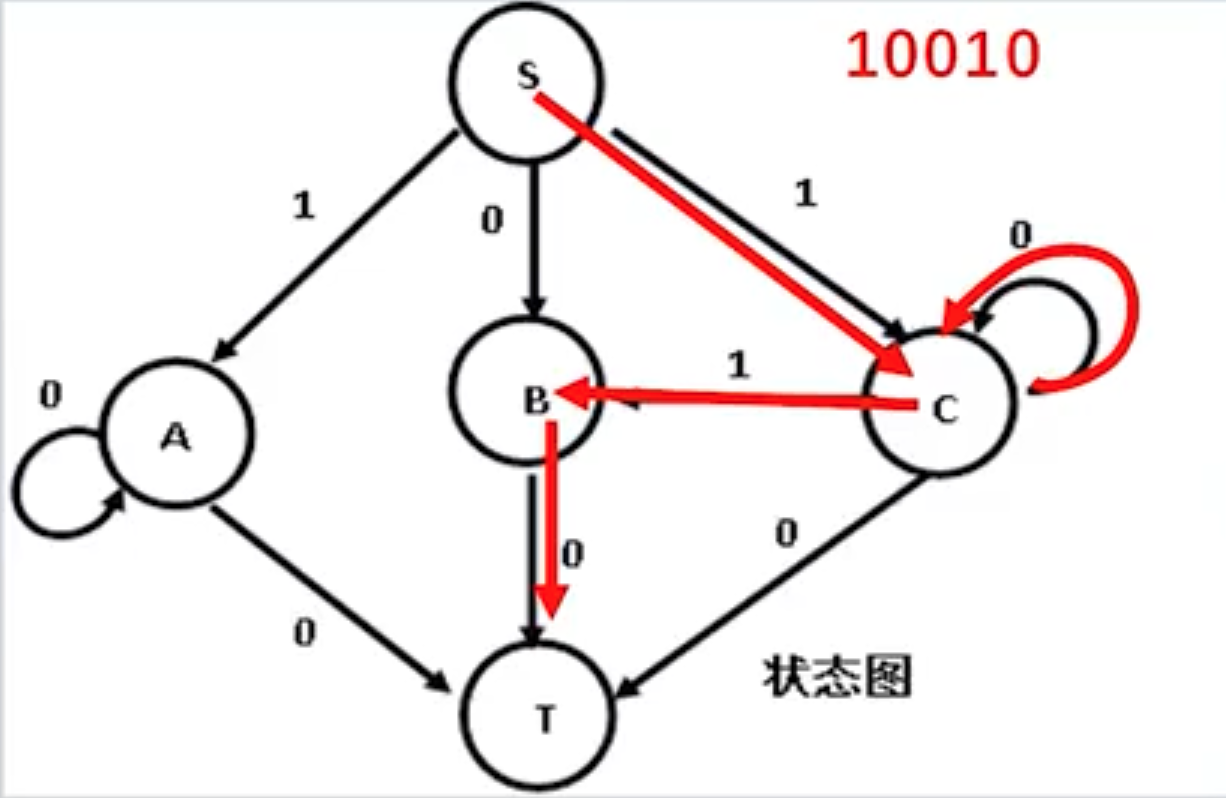 |
| 填充树法 | 对于上下文无关文法,在每一步时考虑所有可能得文法,直到产生样本或无法产生样本为止(本质上是穷举) | 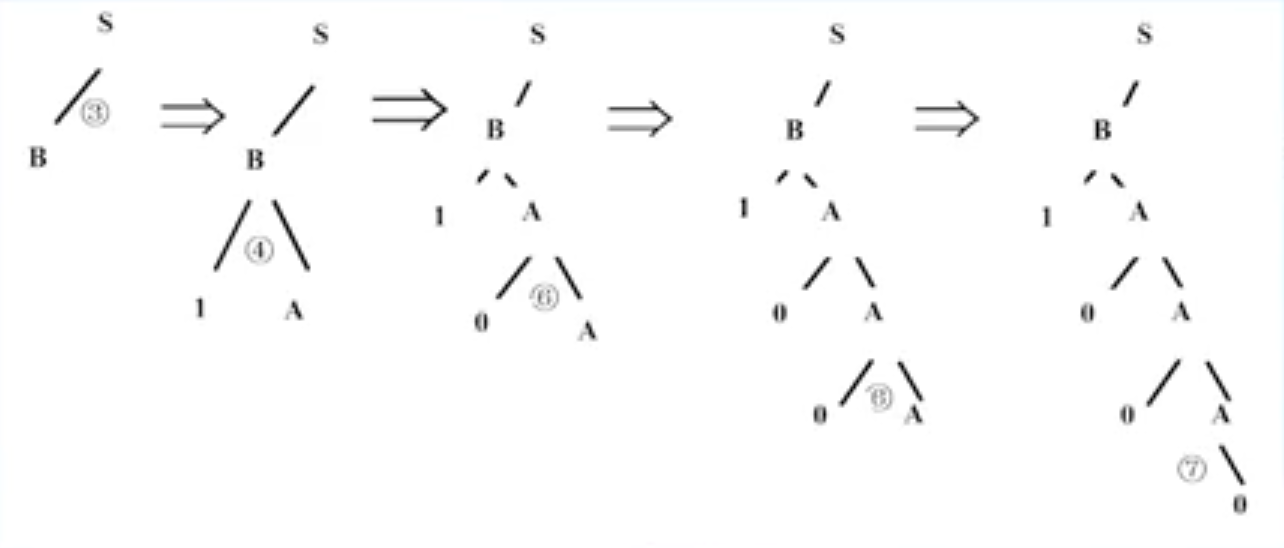 |