图同构:问题最初的定义是只考虑拓扑关系,不考虑节点信息(可以用GNN)
Self-paced Learning:(基于Loss)自适应地动态衡量样本学习难度
Key Idea #
- 实例特征和层次类别特征的统一表达
- 考虑层次结构和实例特征的难度估计(从易到难)
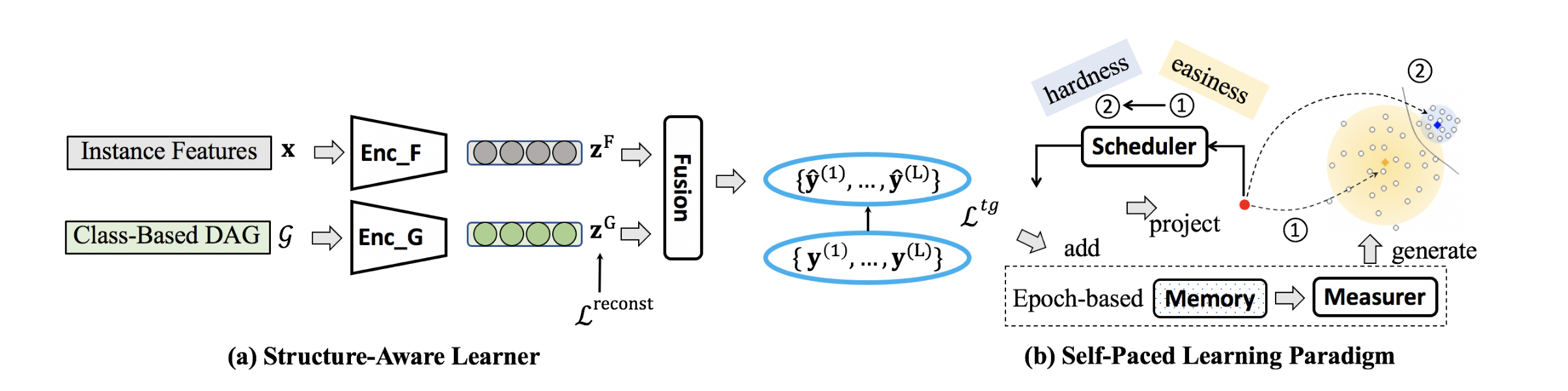
基于Text Embedding和Label Embedding来计算类别概率,并且采用扁平化的方法来完成层次多标签预测 $$ \hat{y} = Sigmoid(W_2(W_1[Z^F||Z^G]+b_1)+b_2) $$
$$ L_{tg} = CE_Loss(y,\hat{y}) $$
避免了MC Loss,而是直接对Label Embedding施加来自Hierarchy的约束(相邻节点互信息最大化),使用可学习的label embedding来避免计算量大的无效的图编码器计算。 $$ L^{reconst}=-\frac{1}{|C|^2}\Sigma_{u \in C}\Sigma_{v \in C}(vu^T-A_{uv}) $$ 根据每一层级的Loss来可导地计算每个样本的难易程度(与平均Loss的差),并通过正则项和Loss权重来实现动态的由易到难。
训练前期,简单样本占主导地位,随着$\lambda$增大,难样本可以在训练初期得到更多的学习。$\lambda=0$是最优。 $$ w_x = \Pi^{L}_{l=1}[1-Sigmoid(L^{(l)}-\hat{L}^{(l)})] $$
$$ min\ Loss(Y,X|W, \lambda)= \Sigma_{x \in X} w_xL_x - \lambda \Sigma_{x \in X}w_x $$