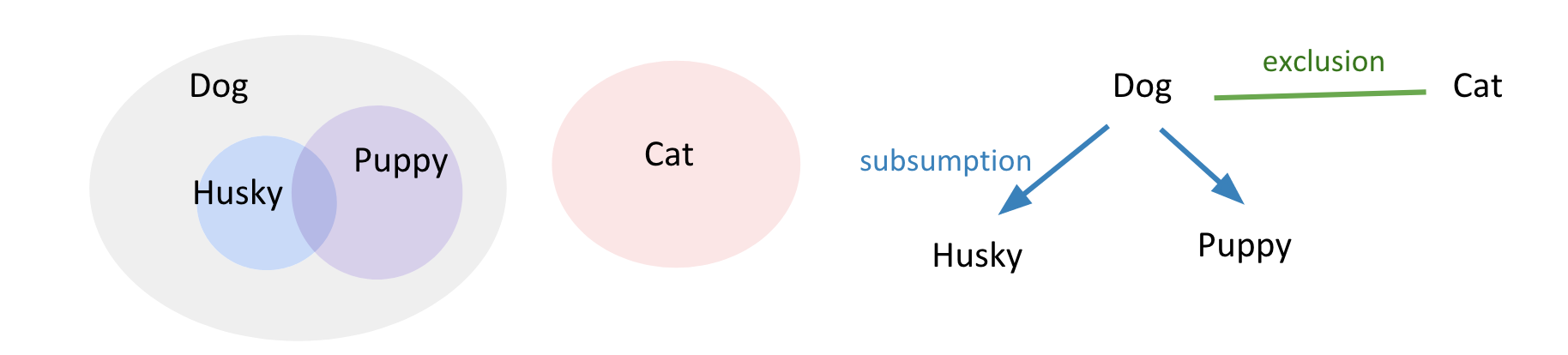
指出了类别标签之间的关系:互斥、包含。
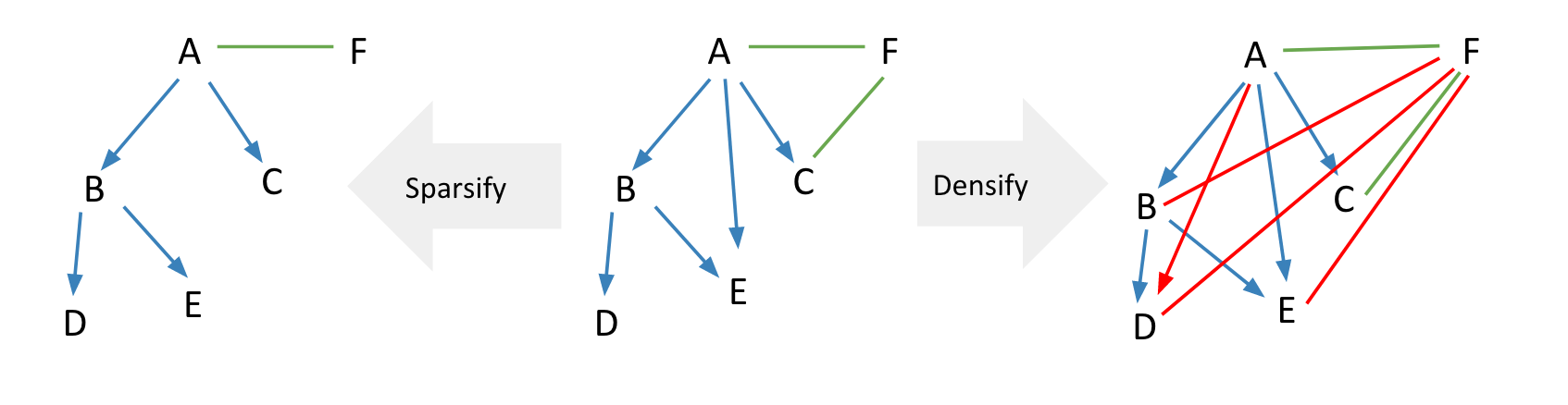
这种关系的建模既可以简单化,也可以复杂化。
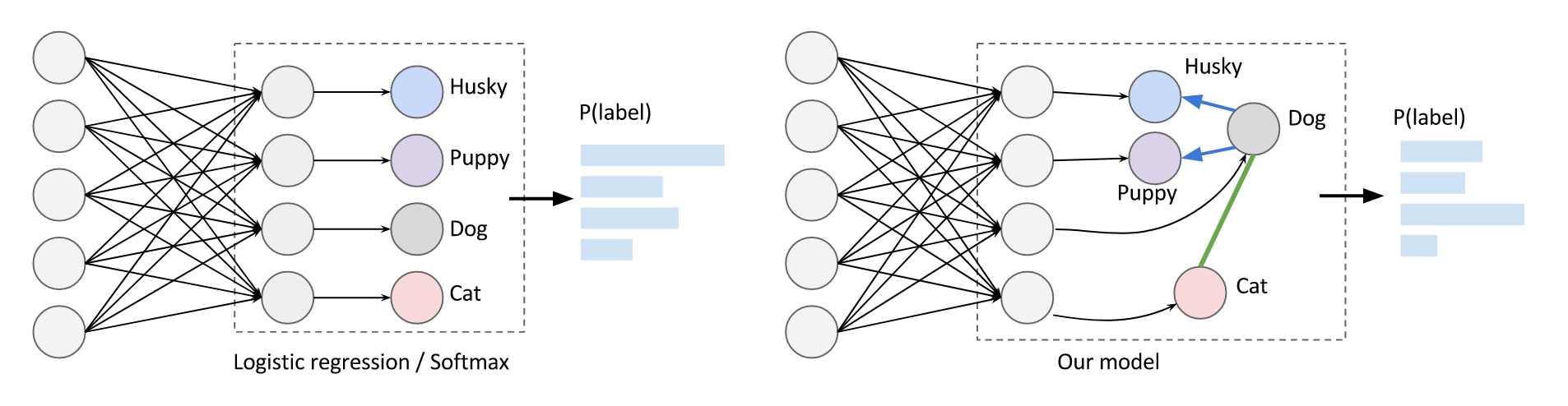
本文的基本思想是对类别标签进行更细粒度的建模:使用神经网络捕获与类别无关的属性,再根据每个类别的先验知识去建模每个类别的概率。 $$ P(y|x)=\prod{e^{f_i(x;w)[y_i=1]}}\prod_{(v_i,v_j)\in E_h}{[(y_i,y_j)\neq(0,1)]}\prod_{(v_i,v_j)\in E_e}{[(y_i,y_j)\neq(1,1)]} $$ 神经网络建模的是属性的联合概率,而当父类为0子类为1、互斥的属性同时为1时,联合概率则被置为0。
对于叶节点,其边缘概率是相关属性的联合概率;对于非叶节点,其边缘概率是其叶子结点的概率和。 $$ L(D,w)=-\sum_{l}{logP_r(y_i|x;w)} $$ 其中,i是标签的索引,如果该标签不属于叶节点,通常可以进一步拆开为若干叶节点的概率和。
基于ImageNet有一个比赛,从2010年开始举行,到2017年最后一届结束。该比赛称为ILSVRC,全称是ImageNet Large-Scale Visual Recognition Challenge,每年举办一次,每次从ImageNet数据集中抽取部分样本作为比赛的数据集。
本文使用ILSVRC2012作为Benchmark,该数据集包含1000类、1.2M图像,这些类别标签可以通过WordNet来建立关系图,并且是DAG而不是Tree,例如狗同时属于犬和家畜。
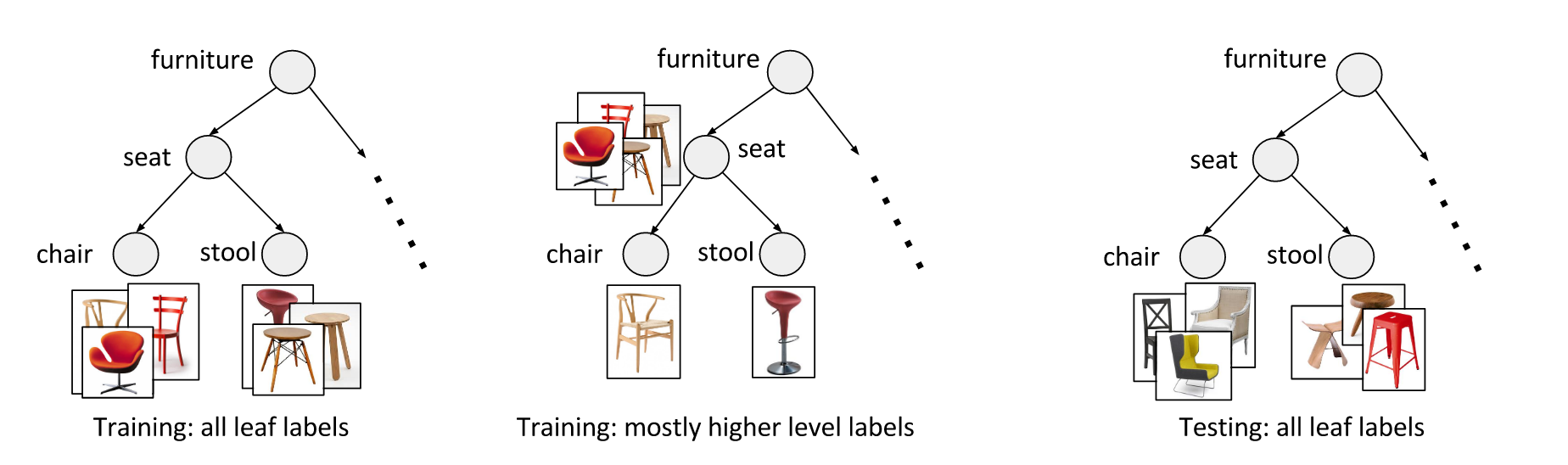
为了探讨本文方法对标签粒度的依赖,本文将一些叶节点标签重新标记为更高层级的标签,并使用这些标签进行训练,但必须指出,每个样本始终只有一个标签;在推理时则使用叶节点作为Ground Truth。
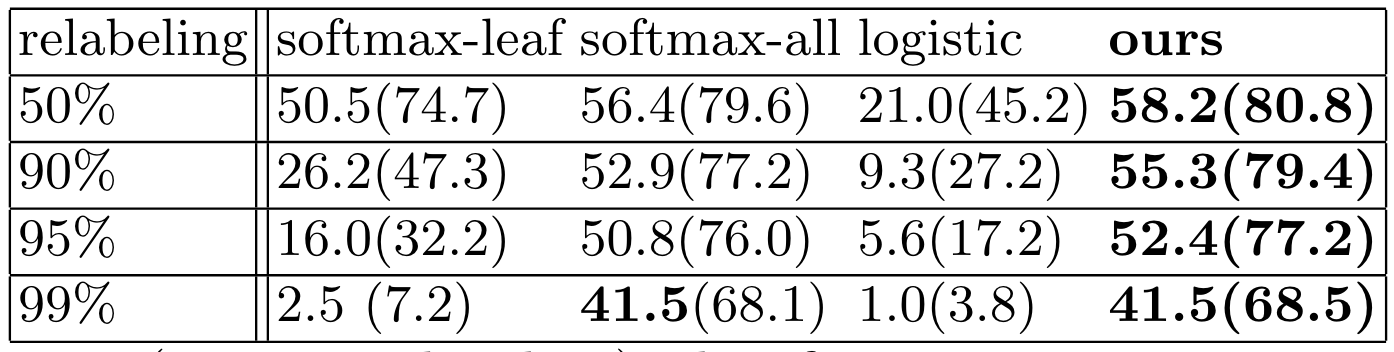
Softmax-leaf忽略所有的高层级标签,Softmax-all将不同层级的标签认为是互斥的,逻辑回归则认为所有标签独立。
显然,本文方法只使用99%的粗粒度+1%的细粒度标签,仍然能取得最优的性能。

AWA数据集包含了50种动物和85种属性,本文方法基于85种属性进一步预测50种动物的概率。在训练时,使用40种动物作为类别标签,并隐式地习得这些属性的建模;在推理时,引入全部50种动物的属性-动物图,以实现未见类的zero-shot推理。
在这两个数据集中,神经网络的预测可以是类别标签的得分,也可以是属性的得分,而前者也被视为一种广义的属性。因此,本文方法具有非常强的启发意义。